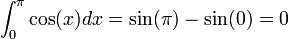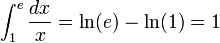domingo, 5 de junio de 2016
miércoles, 25 de mayo de 2016
Máximo absoluto
Una función tiene su máximo absoluto en el x = a si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.
Mínimo absoluto
Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.
a = 0
b = 0
Máximo y mínimo relativo
Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a.
Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.
DEFINICIONES
TEOREMA:
Un teorema es una afirmación que puede ser demostrada como verdadera dentro de un marco lógico a la ves logra ser afirmación que puede ser demostrada verdadera dentro de un marco lógico.
Un teorema generalmente posee un número de condiciones que pueden ser enumeradas en los teoremas o aclaradas de antemano. Luego existe una conclusión, una afirmación matemática, la cual es verdadera bajo las condiciones en las que se trabaja. El contenido informativo del teorema es la relación que existe entre la hipótesis y la tesis o conclusión.
Un teorema generalmente posee un número de condiciones que pueden ser enumeradas en los teoremas o aclaradas de antemano. Luego existe una conclusión, una afirmación matemática, la cual es verdadera bajo las condiciones en las que se trabaja. El contenido informativo del teorema es la relación que existe entre la hipótesis y la tesis o conclusión.
PRIMITIVA:
El concepto de primitiva es el recíproco al de derivada. Se llama función primitiva de otra dada a la original que al derivarla nos da esa otra. “se dice que una función F es una antiderivada o primitiva de f, en un intervalo I si F´(x)=f(x) para todo x en I” Si F es una antiderivada f en un intervalo I, entonces la antiderivada más general de f en I es:F(x) + C
función primitiva
una función primitiva es aquella que después de haber sido derivada pasando por su diferencial y por el proceso de integración no vuelve exactamente a su función original.
PAGINA:
http://www.buenastareas.com/ensayos/Definicion-Funcion-Primitiva/292484.htmlDERIVADA:
En matemática, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.
PAGINA:https://es.wikipedia.org/wiki/Derivada
CONCEPTO DE ANTIDERIVADA:
La antiderivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
Por ejemplo:
Si f(x) = 3×2, entonces, F(x) = x3, es una antiderivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).
La antiderivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.
PAGINA:http://calculodiferencialgrupo501.blogspot.mx/2012/02/concepto-de-antiderivada_22.html
Si f(x) = 3×2, entonces, F(x) = x3, es una antiderivada de f(x). Observe que no existe una derivada única para cada función. Por ejemplo, si G(x) = x3+ 5, entonces es otra antiderivada de f(x).
La antiderivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde: f(x) es el integrando; dx, la variable de integración o diferencial de x y C es la constante de integración.
PAGINA:http://calculodiferencialgrupo501.blogspot.mx/2012/02/concepto-de-antiderivada_22.html
EVALUAR
Una relación matemática puede expresarse como un conjunto de pares ordenados (x, y). Los elementos de estos pares ordenados satisfacen alguna condición matemática previamente establecida entre ellos.
Cuando un conjunto de pares ordenados satisfacen la condición: "a cada valor de x le corresponde un único valor de y", se dice que ese conjunto de pares ordenados representan a una función y cuando se tiene ese caso, "y" se representa como f(x), esto es: y = f(x). Por ejemplo, la relación que se expresa: {( 1, 2 ), ( 2, 4 ), ( 3, 6 ), ( 4, 8 ),...}, satisface la condición: "el valor de y es el doble del valor de x". Representa una función porque a cada valor de "x" le corresponde un solo valor de "y".
Por lo que, para los valores de x = 1, 2, 3, se tiene:
y = f(x) = 2x
f(1) = 2( 1 ) = 2  y = 2
y = 2
f(2) = 2( 2 ) = 4  y = 4
y = 4
f(3) = 2( 3 ) = 6  y = 6
y = 6
El siguiente ejemplo permite analizar la función y = f ( x ) = x2 - 3 donde los valores de "x" son: -2, 0, 1, 2.
.
PAGINA: http://www.cca.org.mx/profesores/cursos/matematicas/hb028/ged/areas/mate/ecuacion/ev_func.htm
Teorema fundamental del cálculo
El teorema fundamental del cálculo consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas.1 Esto significa que toda función acotada e integrable (siendo continua o discontinua en un número finito de puntos) verifica que la derivada de su integral es igual a ella misma. Este teorema es central en la rama de las matemáticas denominada análisis matemático o cálculo.
El teorema es fundamental porque hasta entonces el cálculo aproximado de áreas -integrales- en el que se venía trabajando desde Arquímedes, era una rama de las matemáticas que se seguía por separado al cálculo diferencial que se venía desarrollando por Isaac Newton, Isaac Barrow y Gottfried Leibniz en el siglo XVIII y dio lugar a conceptos como el de las derivadas. Las integrales eran investigadas como formas de estudiar áreas y volúmenes, hasta que en ese punto de la historia ambas ramas convergieron, al demostrarse que el estudio del "área bajo una función" estaba íntimamente vinculado al cálculo diferencial, resultando la integración, la operación inversa a la derivación.
Una consecuencia directa de este teorema es la regla de Barrow,2 denominada en ocasiones segundo teorema fundamental del cálculo, y que permite calcular la integral de una función utilizando la integral indefinida de la función al ser integrada.
Primer teorema fundamental del cálculo
Usando la Regla de la cadena obtenemos como consecuencia directa del primer teorema fundamental del cálculo infinitesimal:
Siendo f(t) una función integrable sobre el intervalo [a(x),b(x)] con a(x) y b(x) derivables.
| Demostración del teorema fundamental del cálculo |
| * Lema
Sea
 integrable sobre integrable sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y y
Entonces
Está claro que
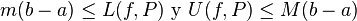 para toda partición para toda partición  . Puesto que . Puesto que  , la desigualdad se sigue inmediatamente. , la desigualdad se sigue inmediatamente.
Por definición se tiene que
 . .
Sea h>0. Entonces
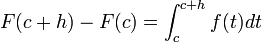 . .
Se define
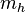 y y 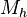 como: como:
Aplicando el 'lema' se observa que:
Por lo tanto,
Sea
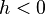 . Sean . Sean
Aplicando el 'lema' se observa que:
Como:
entonces,
Puesto que
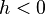 , se tiene que: , se tiene que:
Y como
 es continua en c se tiene que es continua en c se tiene que
y esto lleva a que
|
Ejemplos
| Otra demostración del teorema fundamental del cálculo |
Cogiendo un intervalo cerrado ![[a,x]](https://upload.wikimedia.org/math/a/7/7/a7783208283b6aa11e1a07378a1ae7dc.png) sobre sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ya que , ya que  es continua en es continua en ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , también lo será en , también lo será en ![[a,x]](https://upload.wikimedia.org/math/a/7/7/a7783208283b6aa11e1a07378a1ae7dc.png) . .
Según el teorema del valor medio para integrales se cumple que:
Haciendo el intervalo muy pequeño de tal manera que
 y debido a esa tendencia se tiene también que y debido a esa tendencia se tiene también que 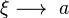
Por lo que en los límites se llega a:
Sabemos que :

Entonces la ecuación se la puede escribir como :
Dado que
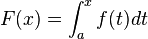 , entonces , entonces 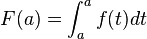
Y debido a que
 es continua en a, entonces es continua en a, entonces 
Vista la ecuación de otra manera:
Por lo tanto
O también
Y en consecuencia
Con ello se demuestra el primer teorema fundamental del cálculo.
|
Segundo teorema fundamental del cálculo
El segundo teorema fundamental del cálculo integral (o regla de Newton-Leibniz, o también regla de Barrow, en honor al matemático inglés Isaac Barrow, profesor de Isaac Newton) es una propiedad de las funciones continuas que permite calcular fácilmente el valor de la integral definida a partir de cualquiera de las primitivas de la función.
Enunciado
|
Demostración del segundo teorema fundamental del cálculo
|
Considérese la siguiente primitiva de  definida en el intervalo definida en el intervalo ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) : :
esto debido al primer teorema fundamental del cálculo el cual establece que:
Como
 y y  son primitivas de son primitivas de  , entonces: , entonces:
Observese que:
y de eso se sigue que
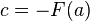 ; por lo tanto, ; por lo tanto,
Y en particular si
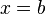 : : |
Ejemplos
Como se puede integrar inmediatamente.
Pagina;https://es.wikipedia.org/wiki/Teorema_fundamental_del_c%C3%A1lculo
Pagina;https://es.wikipedia.org/wiki/Teorema_fundamental_del_c%C3%A1lculo
Suscribirse a:
Entradas (Atom)











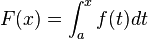



![m \leq f(x) \leq M \; \forall x \in [a,b]](https://upload.wikimedia.org/math/1/e/1/1e1b2ad811ce2c15f191c634ded2afd9.png)

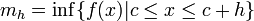 ,
,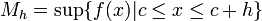
 .
.
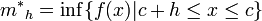 ,
,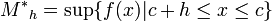 .
. .
.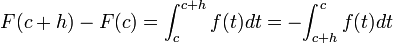 ,
, .
.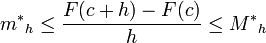 .
. ,
,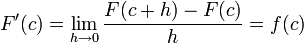 .
.


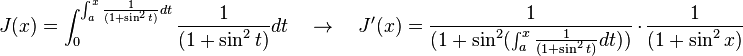
![\exists \xi\in[a,x]
: \quad
f(\xi)=
\frac{1}{x-a}\int_{a}^{x}f(t)dt](https://upload.wikimedia.org/math/f/c/c/fcc1b09852259ebc9a49ff937d0fe4ca.png)





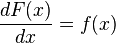


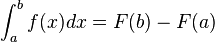
 .
.![G'(x)=f(x) {\ } \forall x \in [a,b]](https://upload.wikimedia.org/math/c/1/c/c1c5b14eec3a07078372ecbb92a559e5.png) .
.![\exists C \in \mathbb{R}: {\ }G(x)=F(x)+C, {\ } \forall x \in [a,b]](https://upload.wikimedia.org/math/b/7/7/b7724a98dad3e4e2b5116f519cf5708c.png) .
.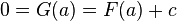
 .
.